Qu'est-ce-qu'une fractale ?
Etymologie
Le mot "fractale" vient de l'adjectif latin fractus qui signifie irrégulier ou brisé.
Définition
La géométrie fractale s'est développée majoritairement avec l'expansion des ordinateurs.
Elle sert à décrire les objets dont les formes laissent apparaître des motifs similaires à des échelles d'observation de plus en plus petites.
Ainsi, les fractales sont des figures invariantes par changement d'échelle (nous parlons aussi de "structures autosimilaires") et sont la représentation graphique de suites récurrentes.
Les fractales permettent de décrire les phénomènes naturels qui présentent une certaine irrégularité, d'où l'appellation de << géométrie de la nature et du chaos >>.
Origine d'apparition
Les fractales sont apparues au 19e siècle ( mais pas sous le nom de fractales, terme introduit dans les années 1970 ), mais jusque vers les années 1970, elles étaient difficilement étudiées et peu comprises; c'est le mathématicien Benoît Mandelbrot qui a été le premier à les expliquer.
Pour voir sa biographie, cliquez ICI.
Je vous ai fait également l'historique d'apparition des fractales ICI.
On y voit que les Fractales sont issues d'un processus long, très long !
Propriétés de certaines fractales
Une dimension non euclidienne ==> aire finie pour un périmètre infini !
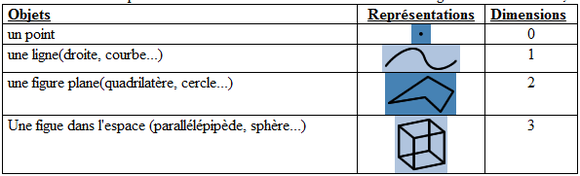
En dimension euclidienne, les dimensions données sont exclusivement entières.
En voici un rappel :
Cependant si nous prenons par exemple la courbe de Koch, nous constatons que lorsque nous multiplions sa dimension par 3, nous contatons que la courbe de Koch a en faite été multipliée par 4 !
Constatez par vous-même :
Si la courbe de von Koch était de dimension 1, alors sa mesure serait multipliée par 3.
Si la courbe de von Koch était de dimension 2, alors sa mesure serait multipliée par 9.
Or sa mesure vaut 4; sa dimension est donc comprise entre 1 et 2 !
Pour trouver sa dimension "d" exacte, il faut résoudre l'équation :

L'idée est le sortir la puissance d grâce aux propriétés sur le logarithme népérien :

Remarque :
On aurait aussi pu passer par le logaithme décimal log( ), maic c'est strictement équivalent.
En effet :

Votre courbe de Koch a ainsi une dimension d'environ 1.26 !
ATTENTION
Le périmètre de la courbe de Koch est infini !
http://www.siteduzero.com/sciences/tutoriels/les-dimensions-en-geometrie/figures-autosimilaires
Pour comprendre que la longueur de la figure est de longueur infinie, on peut raisonner de la façon suivante. À chaque étape, on remplace chaque segment par 4 petits segments qui ont une longueur égale à 1/3 de la longueur du segment de base. Autrement dit, à chaque fois, la longueur de la figure est multipliée par 4 imes (1/3)=4/3\approx 1,333.... Ainsi, si on part d'un segment de longueur 1 à l'étape 0, alors à l'étape n, la figure a une longueur égale à (4/3)^n. Plus n est grand, plus cette longueur est grande, de telle sorte qu'à l'infini, la longueur de la courbe est infinie !
Utilité de la dimension fractale
Un tronc d'arbre ressemble à un cylindre, une orange à une sphère. Mais la géométrie Euclidienne connaît ses limites quand on essaye de définir des formes plus complexes comme des montagnes, des nuages, ou même des choux-fleurs... C'est là que la géométrie fractale intervient.
Une autosimilarité
L'autosimilarité est le caractère d'un objet dans laquelle on peut trouver des similarités en l'observant à différentes échelles.
L'ensemble de Mandelbrot est un bon exemple de Fractale autosimilraire :
La courbe de Koch est un autre exemple de Fractale autosimiliaire.

Dans la vie de tout les jours, les autosimilarité sont présentes là où l'on sy attend le moins :
Pour la vache qui rit, on appelle cela une mise en abyme (figure de style).
Conférence avec Mandelbrot en personne
http://www.ted.com/talks/benoit_mandelbrot_fractals_the_art_of_roughness.html
Je vous oblige à aller voir ce reportage d'Arte sur les fractales.
Vous y cernerez mieux le sujet et vous y découvriez plein de nouveautés.
Vous verez, vous n'allez pas être déçu du voyage !
 A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?
A la découverte des (Hyper)complexes,
des fractales ET de la théorie du Chaos
Sont-ils présents dans notre monde ?